De site van NedCAD

Orthorectificatie: 2D versus 3D

By nedcadPosted on Posted in Blog, GIS

Let op, dit is een concept.

“Orthorectificatie” (“orthorectografie”) kan je omschrijven als het ontdoen van perspectief in een foto waardoor een exact haaks bovenaanzicht ontstaat met een kloppende x- en y-schaal. Als gevolg kan zo’n “gerectificeerde” foto geplaatst worden in een CAD-programma. Je krijgt dan een platte projectie waarin je kan meten, de foto is op de juiste schaal. Dit proces kan gezien worden als een onderdeel van fotogrammetrie.

In het Nederlands, en andere talen, zijn er soms geen termen beschikbaar. Daarom worden de volgende termen gebruikt:
Orthorectification (Engels)
Van “haaks” en “richten”, haaks uitlijnen, orthorectificatie (~Anglicisme), haakse of loodrechte correctie of uitlijning. Feitelijk is “orthorectificatie” een Latinisme van “ortho” als in haaks en “rectificatie” als in correctie, aanpassing. Het resultaat van orthorectificatie bestaat uit een “orthofoto”.

Introductie

Sommige programma’s om foto’s te ontdoen van hun perspectief negeren 3D-coordinaten, ze gebruiken alleen 2D-coordinaten zodat de foto uiteindelijk een betrouwbaar beeld geeft van een bovenaanzicht. Dat is in veel gevallen voldoende.

Echter, CAD-gebruikers dienen ervan bewust te zijn dat deze foto’s niet bruikbaar zijn in afgeleide coördinaatsystemen (User Coordinate System, UCS). Meer precies, in een UCS parallel aan het wereldcoördinaatsysteem (WCS) zijn dergelijke foto’s prima te gebruiken maar als de hoek tussen de z-as van het WCS en het UCS groter wordt, dan wordt de afwijking ook groter. Die hoek is belangrijk en bepaalt of de fout acceptabel is of zelfs totaal onacceptabel is. Het eventuele criterium daarbij is een procentuele foutmarge.

In de werkelijke, niet platte, wereld dient een foto goed gepositioneerd te worden, dwars door de punten die verzameld zijn middels bijvoorbeeld een total station. Meestal worden hier per foto vier (4) punten voor gebruikt en daarmee ontstaat meteen een dilemma. Immers, die vier punten liggen wel min of meer in één vlak maar nooit exact in één vlak.

Dit probleem is op twee manieren op te lossen:

  • Methode I, vier-punts orthorectificatie: Laat de foto “zo goed mogelijk” samenvallen met de vier punten:
    • Haaks op de foto kijkende vallen alle (vier) referentiepunten in de foto samen met de vier gemeten punten. Echter,
    • Evenwijdig aan de foto kijkende zal geen enkel coördinaat samenvallen met de foto. De foto zal echter wel door een virtueel vlak lopen waarbij een zo klein mogelijke en gemiddelde afwijking de locatie van dat virtuele vlak in de ruimte bepaalt.
    • Dit vereist een nieuw wiskundig algoritme, zie hierna.
  • Methode II, drie-punts orthorectificatie: Vier punten vormen een vierhoek. In die vierhoek passen twee driehoeken. Laat de foto exact samenvallen met die driehoeken.
    • Het betekent dat de foto twee keer geplaatst wordt waarbij iedere foto samenvalt met een driehoek en met een snijlijn (ImageClip) over de diagonaal van de vierhoek.
    • Om en nabij het midden van die diagonaal zal er alsnog een fout aanwezig zijn en driehoeken kan je op twee manieren plaatsen:

De implementatie van bovenstaande twee methoden vereisen controle over de gebruikte API van de CAD-omgeving en de orthorectificatie-omgeving.

  • Methode III, coördinaatmanipulatie: Een derde methode bestaat uit het “manipuleren” van bestaande orthorectificatie-software. Die software werkt goed in 2D. Het is wiskundig mogelijk om vier 3D-punten “plat te slaan” zoals hiervoor beschreven bij de “vier-punts orthorectificatie”. Er ontstaat dan een nieuwe set 2D-coördinaten die als invoer voor die bestaande software gebruikt wordt. Het resultaat zal dan ruimtelijk goed geplaatst moeten worden.

Al met al zijn er mogelijkheden om 3D te benutten om de best mogelijke resultaten te bereiken. Dit is belangrijk omdat de kwaliteit van een CAD-model op een hoger niveau komt te liggen en, belangrijker, om onacceptabele fouten te voorkomen.

Voor wat betreft de wiskunde zijn functies die ik heb beschreven in “Applied Mathematics concerning CAD Faces” onontbeerlijk. Het is een lange post maar de materie is niet extreem moeilijk (wel moeilijk 😉 ). Het doel van deze post is bewust wiskundige methoden en algoritmen publiek en uitlegbaar te maken. Voor we aan de slag gaan eerst een belangrijk intermezzo:

Intermezzo: ijking en vervorming

Orthorectografie zal altijd ijking vereisen waarbij lensparameters overeenkomen met software-instellingen. Als dat gedaan is dan maakt het binnen het proces niet uit onder welke hoek de ondergrond staat. Echter, als z-coördinaten van de referentiepunten onderling veel verschillen, bij een hellend vlak bijvoorbeeld, en als daarbij de software die z-coördinaten negeert, dan kunnen er aanzienlijke en ontoelaatbare vervormingen ontstaan tussen de referentiepunten en buiten de referentiepunten.

Dat is een reden om uitermate zorgvuldig om te gaan met de toepassing van 3D-coordinaten binnen programmatuur die z-waarden negeert.

De beschreven methoden in deze post nemen de z-waarden wel volledig mee waardoor dit probleem niet speelt.

Algoritmen en wiskunde

Coördinaatmanipulatie

Theorie

Dit, methode III, is een logische eerste stap en vormt ook een belangrijke basis voor vier-punts orthorectificatie (methode I).

Het proces is als volgt:

  • Een vierhoek heeft ruimtelijke coördinaten ABCD.
    • Belangrijk om te beseffen is die punten wel ongeveer in één vlak liggen maar in de praktijk nooit exact in één vlak liggen.
    • We zoeken dus een methode waarbij dat vlak zo gedefinieerd wordt dat de afwijking, de afstanden van de punten tot dat vlak, minimaal is.
    • Er zijn meerdere wiskundige methoden te bedenken om dit probleem op te lossen. De keuze is als volgt:
      • Het vlak loopt exact door het gemiddelde van alle coordinaten (afb. rechts). Dit is punt Q. Q kan ook geformuleerd als het midden tussen de middens van de diagonalen (afb. midden).

      • De hoek van het vlak wordt bepaald door het gewogen gemiddelde van normalen van de nieuwe driehoeken die allemaal een hoekpunt Q hebben.

Daarmee hebben we de methodiek te pakken en dit is beargumenteerbaar de beste methode om de marges te minimaliseren. Goed om te beseffen is dat het vlak eenduidig in de ruimte ligt door punt Q en de richting van de uiteindelijke normaalvector.

  • Punt Q is bepaald. Dit levert 4 driehoeken op: AQB, BQC enzovoorts.
  • Van alle driehoeken kunnen normalen bepaald worden volgens de rechterhandregel:
    \vec {QA} \times \vec {QB} dan \vec {QB} \times \vec {QC} enzovoorts, zie Calculate the normal of a face.
    • Deze normalen liggen dicht bij elkaar qua richting.
    • De magnitude van een normaal komt overeen met het oppervlak van zo’n driehoek en is daarmee een maat voor het “gewicht” van iedere normaal op de gemiddelde vector, richting.
  • Er wordt vervolgens een gemiddelde normaal bepaald.
  • Om de geprojecteerde coördinaten in een plat vlak te bepalen kan de gemiddelde normaal verdraaid worden over een (ruimtelijke) hoek, zodanig dat de normaal samenvalt met de z-as. Vervolgens kunnen de coördinaten over dezelfde hoek gekanteld worden. De nieuwe x- en y-coördinaten van ABCD vormen de plat, haaks, geprojecteerde coördinaten. Dit proces levert enkele uitdagingen op:
    • Een verdraaiing van coördinaten om een punt staat hier beschreven: Calculate rotation of a coordinate in 2D. Door eerst een 2D-verdraaing evenwijdig aan het x-z-vlak uit te voeren en daarna een verdraaiing over het y-z-vlak uit te voeren verkrijgen we in twee stappen de 3D-verdraaiing.
    • Het punt waarover verdraaid wordt (“base point”) is het punt “Q” van de vierhoek, het midden tussen de middens van de diagonalen als hierna, het gemiddelde van de coördinaten van ABCD.
  • Dan volgt de eindfase:
    • De gevonden geprojecteerde x- en y-coördinaten kunnen (al dan niet getransleerd) verder verwerkt worden in het fotogrammetrie-programma.
    • ABCD ligt niet in een vlak. In de geprojecteerde toestand kunnen punten A’, B’, C’ en D’ gedefinieerd worden door ze allemaal de z-coördinaat van punt Q te geven. Door nu A’B’C’D’ terug te draaien ontstaan iets aangepaste meetpunten die echter wel exact in één vlak liggen waarbij dat vlak precies door het punt Q loopt.
    • Zie bijvoorbeeld deze post met codes voor bitmaps. De bitmap kan vervolgens met de juiste DXF-codes ingevoegd worden, de waarde van het invoegpunt en de U- en V-vectorwaarden van de nieuwe bitmap zijn immers voorhanden. De verwerkte bitmap zou eventueel begeleid kunnen worden met een bestand met een identieke naam voorzien van metadata.
Intermezzo: Optimalisatie

Wiskundige zaken kunnen eventueel geoptimaliseerd worden in een later stadium. Enkele voorbeelden die hier zo toegepast kunnen worden:

\sin (\arctan x) = \frac{x} {\sqrt{1+x^2}}

\cos (\arctan x) = \frac{1} {\sqrt{1+x^2}}

Echter, gezien de wiskundige complexiteit van de hier beschreven procedure enerzijds en anderzijds het feit dat de berekening slechts enkele malen uitgevoerd dient te worden – afhankelijk van het aantal foto’s – is het aan te bevelen de bijbehorende softwarecode niet al te veel te laten afwijken van het praktijkvoorbeeld hierna, met bewust minder optimalisatie dus.

Vooruitlopend op onderstaande gebruik ik zowel een CAD-model (.dwg) als een Open Document-rekenblad om er zeker van te zijn dat wat ik hier publiceer ook klopt. [ref orthorect<n>.dwg, orthorect.ods]

Het voordeel van een rekenblad is dat er meteen een raamwerk aanwezig is voor de uiteindelijke flow van programmacode en de daarbij behorende formules.

Praktijk

Op basis van een fictief voorbeeld wordt het bovenstaande uitgevoerd.

De normaalvector

Hieronder staat een voorbeeld tot en met de normaalvectoren:

  • Punten ABCD liggen net niet in één vlak. Coördinaten:
    A:10,10,5
    B:30,10,10
    C:30,45,35
    D:10,35,30
  • Het punt Q is het gemiddelde van die coördinaten:
    Q:20,25,20
  • Er zijn vier driehoeken zichtbaar, AQB, BQC, CQD en DQA.
  • Vier vectoren spelen een rol:
    QA:-10,-15,-15
    QB:10,-15,-10
    QC:10,20,15
    QD:-10,10,10
  • Normaalvectoren zijn getekend als 20% van werkelijke magnitude.
  • De volgende kruisproducten vormen een normaal (magenta) vertrekkend vanaf punt Q van iedere driehoek:
    \vec {QA} \times \vec {QB}: -75,-250,300
    \vec {QB} \times \vec {QC}: -25,-250,350
    \vec {QC} \times \vec {QD}: 50,-250,300
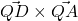    \vec {QD} \times \vec {QA}: 0,-250,250
  • De gemiddelde normaalvector (vertrekt vanaf punt Q):
    -12.5,-250,300
  • Magnitudes en gewichten:
    Hierna is geen rekening gehouden met de gewichten, de invloed op de richting, van de normalen van de vier driehoeken. Het is een verfijning die in de software wel verwerkt wordt. Uitleg:
    • Magnituden van iedere normaalvector:
      |\vec{Naqb}| = \sqrt{(-75)^2+(-250)^2+(300)^2}=397.65
      |\vec{Nbqc}| = \sqrt{(-25)^2+(-250)^2+(350)^2}=430.84
      |\vec{Ncqd}| = \sqrt{(50)^2+(-250)^2+(300)^2}=393.7
      |\vec{Ndqa}| = \sqrt{(0)^2+(-250)^2+(250)^2}=353.55
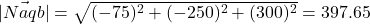
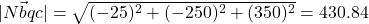
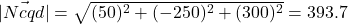
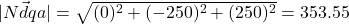
    • De som van deze waarden gedeeld door 4 geeft een gemiddelde.
    • Iedere magnitude delen door het gemiddelde levert een factor, een “gewicht” op in de buurt van 1.
    • Iedere hiervoor berekende normaalvector dient vermenigvuldigd te worden met die factor. Hier is een functie lv:multiply voor beschikbaar. De nieuwe gewogen normaal wordt zo berekend en vormt de gemiddelde definitieve normaalvector.
    • Het gaat te ver om dit uit te werken hier maar de conclusie is wel interessant: Het verschil tussen de gemiddelde normaalvector en de gewogen gemiddelde normaalvector levert een verbetering op van, in dit voorbeeld, 0.25 graden. Dit betekent dat een foto met een breedte van 10 m aan de uiteinden zo’n 20 mm hoger of lager ligt. In de praktijk zal dit vaak minder zijn, afhankelijk van hoe nauwkeurig de meetpunten in een vlak liggen.
De verdraaiing, het concept

De volgende stap is de verdraaiing van de punten en de normaalvector, zodanig dat de x- en y-coördinaat van de normaal (0,0,m) wordt waarbij m de magnitude is. Dat laatste impliceert dat de lengte van de vector gelijk blijft.

Deze afbeelding is voorzien van de xyz-assen, rood groen blauw, RGB. Het x-z-vlak is het vlak dat loopt door de rode en blauwe as. x-y-vlak: rood en groen en y-z-vlak groen en blauw. Door Q lopen twee draaiassen, rood en groen.

Het is belangrijk om te beseffen dat iedere verdraaiing op zichzelf staat en het geheel neerkomt op het twee keer verdraaien van een vaste, onderling verbonden, groep van punten en vectoren over een denkbeeldige as door punt Z. Bij de eerste verdraaiing om punt Z veranderen niet alleen de coördinaten van ABCD, maar ook de normaalvector (magenta). Omdat de normaal verandert, verandert ook de tweede draaihoek. Dat is de reden om de gehele verdraaiing uit te voeren in twee delen, eerst in het x-z-vlak om een denkbeeldige as (groen) die door Q loopt, haaks op het x-z-vlak. De tweede verdraaiing is dan op basis van de nieuw verkregen (tijdelijke) punten en een gewijzigde normaalvector: een verdraaiing in het x-y-vlak om de denkbeeldige as (rood) die door Q loopt, maar dan haaks op het x-y-vlak.

Eerste verdraaiing in x-z-vlak…
Eerste verdraaiing
  • Normaalvector: (-12.5,-250,300)
    • Het x-z-vlak: De hoek van de normaalvector:
      α=atan(Nx/Nz)
      =atan(-12.5/300)=~0.04164 rad.
  • De verdraaiing α van ABCD over Q: De vectoren QA … QD staan hierboven. Vectoren als QAr1, eerste (1) rotatie, er volgt immers nog een verdraaiing.
    • QAr1=QAx*cos(α)-QAz*sin(α),QAy,QAy*cos(α)+QAx*sin(α)
    • QBr1=QBx*cos(α)-QBz* … etc.
    • Vectoren:
      QAr1: (-10.61,-15,-14.57)
      QBr1: (9.57,-15,-10.40)
      QCr1: (10.61,20,14.57)
      QDr1: (-9.57,10,10.40)
Tweede verdraaiing
  • Voor de tweede verdraaiing hebben we een hoek nodig van de normaalvector in het x-y-vlak: β=atan(Ny/Nz).
    • Daarvoor zullen we eerst de normaalvector moeten verdraaien over Q met hoek α:
      Nr1=Nx*cos(α)-Nz*sin(α),Ny,Ny*cos(α)+Nx*sin(α)
      Vector:
      Nr1: (0,-250,300.260303736608)
      Een andere benadering: Als x=0 dan is de z-waarde volgens Pythagoras waarbij y gelijk blijft:
      Nr1=0,-250,sqrt(Nx^2+Nz^2)
    • De hoek weten we dus nu:
      β=atan(Ny/Nz)=atan(-250/(sqrt -12.5^2+300^2))=
      ~0.6943 rad.
  • Daarmee zijn we toe aan de verdraaiing van ABCD over Q met hoek β.
  • In de figuur zie je de verdraaiing van normaalvector Nr1 naar Nr met hoek β. Je ziet bij punten ABCD ook de eerder verdraaide vectoren Ar1, Br1,… (cyaan, zonder aanduiding). Die laatste vectoren worden nu gedraaid over Q met hoek β. Het resultaat bestaat uit de punten Ar2, Br2, Cr2 en Dr2 met bijbehorende vectoren QAr2, QBr2, … Dit is de uiteindelijke situatie waarbij de punten zo goed mogelijk in één vlak liggen. Je ziet dat het in dit geval afwijkt, maar beter krijg je het simpelweg niet. Iemand met een total-station zal altijd zijn meetpunten zo goed mogelijk in één vlak opnemen, aanzienlijk beter dan ik in dit voorbeeld doe.
  • Bedenk dat ons doel uitsluitend is om AR, BR,… in één vlak te krijgen. Ze erven daarvoor allemaal de z-waarde van punt Q. In de richting van Nr kijkende liggen alle punten dan nog steeds op exact dezelfde locatie met – niet zichtbaar – een kleine aanpassing van de z-waarde.
    • De verdraaiing β van Ar1, Br1, … over Q: De vectoren QAr1 … QDr1 staan hierboven. Dus:
      QAr2=QAr1x,QAr1y*cos(β)-QAr1z*sin(β),QAr1z*cos(β)+QAr1y*sin(β)
      QBr1=QBr1x,QBr1y*cos(β)*cos(β)-QBz* … etc.
    • Vectoren:
      QAr2: (-10.61,-20.85,-1.59)
      QBr2: (9.57,-18.18,1.59)
      QCr2: (10.61,24.69,-1.59)
      QDr2: (-9.571,14.34,1.59)
Middeling z-coordinaten
  • Merk op dat de z-coördinaten hierboven gelijk zijn, behoudens de tekens. Daaruit is te concluderen dat we de best mogelijke middeling met deze methode bereiken. We zetten nu de z-waarde op 0:
    QA3=QAr2x,QAr2y,0
    QB3=QBr2x,QBr2y,0
    etc.
  • Vectoren:
    QA3: (-10.61,-20.85,0)
    QB3: (9.57,-18.18,0)
    QC3: (10.61,24.69,0)
    QD3: (-9.57,14.34,0)
Invoer 2D orthorectificatie
  • In dit lange verhaal zou je haast vergeten dat we nu dus de platgeslagen 2D-coordinaten kunnen bepalen door het zwaartepunt Q er bij op te tellen:
    Ao: (Qx+QA3x,Qy+QA3y)
    Bo: (Qx+QB3x,Qy+QB3y)
    etc.
  • Punten:
    Ao: (9.38,4.14)
    Bo: (29.57,6.81)
    Co: (30.61,49.69)
    Do: (10.42,39.34)
  • Bij meerdere puntenreeksen zal een aanvullende methode gebruikt moeten worden als meerdere foto’s gedeelde referentiepunten gebruiken – feitelijk vectorsommen optellen bij reeds bepaalde punten.
Eerste terugdraaiing
  • Nu moeten we alles weer, in het y-z-vlak, terugdraaien over hoek -β, ofwel ɣ. De formules worden makkelijker want z-coördinaten zijn immers 0:
  • QA4=QA3x,QA3y*cos(ɣ),QA3z*sin(ɣ)
    etc.
  • Vectoren:
    QA4: (-10.61,-16.02,-13.34)
    QB4: (9.57,-13.97,-11.63)
    QC4: (10.61,18.97,15.80)
    QD4: (-9.57,11.02,9.17)
  • Merk op dat deze vectoren heel dicht in de buurt van de vectoren van de eerste verdraaiing dienen te liggen.
  • Ook van de afwijking kunnen we iets zeggen, die is nooit meer dan de gecorrigeerde z-waarde, + of – 1.59 in dit voorbeeld.
Intermezzo: Zekering van kwaliteit, deviatie
  • Fouten zijn menselijk en moeite stoppen in controlemechanismen is waardevol.
  • Nederland lijkt plat maar is het net niet helemaal. Iemand die veel moeite doet om met een total-station 4 punten ABCD op te nemen, die ogenschijnlijk in één vlak liggen, zal altijd een foutmarge moeten accepteren. We kunnen wel degelijk iets zeggen over de marge (bijvoorbeeld in procenten):
    • De magnitude M (lengte) van de gemiddelde normaalvector N is een maat voor het totale oppervlak van vierhoek ABCD. Meer precies, het oppervlak is M*4.
    • De wortel van M*4 is een redelijke benadering voor een gemiddelde indicatieve lengte S tussen de opeenvolgende meetpunten A-B, B-C, … Dus:
      S=\sqrt{M*4}
    • Onder het kopje “Tweede verdraaiing” ontstaan z-coördinaten die de afwijking ten opzichte van een ideaal vlak weergeven in de gedaante “+/-dz”.
    • R is de verhouding van absolute waarde |dz| en S. Daarmee is R een maat voor de zekering van minimale kwaliteit Rmin.
  • Met andere woorden:
    0\leq\frac{|dz|}{\sqrt{M*4}}\leq Rmin
  • Na vastlegging van Rmin kan R gelogd worden en onacceptabele afwijkingen kunnen actief gemeld worden.
Tweede terugdraaiing
  • De tweede en laatste verdraaiing in het x-z-vlak over hoek -α, ofwel δ. We hebben de smaak inmiddels wel te pakken…
  • QA5=QA4x*cos(δ)-QA4z*sin(δ),QA4y,QA4y*cos(δ)+QA4x*sin(δ)
    etc.
  • Vectoren:
    QA5: (-10.05,-16.02,-13.77)
    QB5: (10.05,-13.97,-11.22)
    QC5: (9.94,18.97,16.226)
    QD5: (-9.94,11.02,8.77)
  • Daarmee komen we uiteraard weer heel dicht in de buurt van de allereerste vectoren, visuele controle volgt. Voor de coördinaten dient punt Q opgeteld worden bij de vectoren en zo komen we uit op nieuwe coördinaten voor An, Bn, Cn en Dn:
    An: (9.94,8.97,6.22)
    Bn: (30.05,11.02,8.77)
    Cn: (29.94,43.97,36.22)
    Dn: (10.05,36.02,28.77)
  • THAT’S ALMOST ALL FOLKS!!
Visuele controle
  • We hebben vierhoek ABCD (zwart) en gaan AnBnCnDn (magenta) ook tekenen, als script:
    line
    9.94882292732856,8.97645854657114,6.22824974411464
    30.0511770726714,11.0235414534289,8.77175025588536
    29.9488229273286,43.9764585465711,36.2282497441146
    10.0511770726714,36.0235414534289,28.7717502558854
    close
  • We zien dat de hoekpunten van de magenta lijnen dicht bij de hoeken van de zwarte lijnen liggen. Het geeft nog geen goed beeld van het resultaat en daarom maken we een UCS waarbij de z-as samenvalt met normaalvector (cyaan) bij punt Q. Daarna een Plan-commando en dat levert dit op:
  • Bingo! Dit is het aanzicht waarin de orthofoto gepositioneerd wordt in 3D, op referentiepunten ABCD. Je ziet dat de oorspronkelijke punten ABCD exact samenvallen met de nieuwe (niet benoemde) punten AnBnCnDn. Dat is precies wat we wilden bereiken.
  • Nu moeten we nog controleren of AnBnCnDn in één vlak liggen. We maken een 3-punts UCS op basis van AnBnCn, roteren dat 90 graden over de y-as en doen Plan:
  • Het is misschien niet direct duidelijk maar er is één rechte magenta lijn en dat betekent JACKPOT, punten AnBnCnDn liggen precies op één lijn en dus in één vlak. Wederom exact wat we wilden bereiken. Je kunt ook goed zien hoe goed het magenta vlak precies tussen de punten ABCD gemiddeld is.

Slotopmerkingen

Deze uitgebreide illustratie laat zien en maakt duidelijk dat 2D-orthofoto’s op een betrouwbare en gewenste manier geplaatst kunnen worden in een 3D-omgeving, volledig uitgelijnd op 3D-coordinaten.

Door deze benadering zijn meerdere 2D-orthorectieficatie-programma’s in te zetten in 3D-CAD-omgevingen.

Orthorectificatie: 2D versus 3D
Scroll to top